Quantum Computer Aided Engineering
Classical computation, while powerful, faces limitations in tackling the breadth and complexity of design problems. These limitations are primarily the processing speed and storage capacity of classical devices. In response, quantum computation emerges as a potential solution, possibly revolutionising engineering design. By leveraging quantum phenomena, such as superposition and entanglement, quantum computers could potentially resolve significantly larger design spaces and/or existing design spaces in a fraction of the time. The challenge is refactoring Engineering Design problems to best take advantage of quantum computing as well as understanding the requirements and capabilities of current and future quantum devices.
Computation in Engineering Design
Computational methods have become indispensable tools and revolutionised the process of designing and optimising solutions. 50 years ago, Engineering Design relied heavily on manual calculations, physical prototypes, and intuitive decision-making. Engineers meticulously performed calculations by hand, often spending countless hours computing and evaluating design alternatives. The design process was time-consuming, limited in scope, and heavily dependent on the expertise and intuition of the designers.
This reliance on analytical hand-calculated solutions has significantly diminished as tools like Computational Fluid Dynamics (CFD) and Finite Element Analysis (FEA) software have become standard practices. These digital tools allow engineers to visualise, manipulate, and iterate on designs in a virtual environment, saving time, resources, and reducing the need for extensive physical testing. Moreover, engineers now have access to powerful algorithms, simulations, and modelling techniques that enable them to explore a vast design space and optimise solutions with unprecedented precision.
The design process today can be characterised as a data-driven decision-making process, where engineers are supported by comprehensive analysis, optimisation algorithms, and machine learning techniques to guide their decisions. Designers now have a suite of computational methods that have become integral to Engineering Design. These methods enable designers to discover key information about their problem and its potential solutions. This information ranges from how sensitive a design is to changes in design and/or scenario parameters, what are the number of theoretical solutions, and how optimal is the current solution? The role of the designer is therefore shifting from the generation of solutions to the definition/constraint of design spaces that can then be explored more rapidly through computation and to a much fuller extent.
Problems with the Classical Approach
No matter how well our computational methods perform, designers are always looking to increase the fidelity and expanse of the design space they are exploring. Never satisfied, the primary objective remains to reduce uncertainty and increase confidence in the design taken to production.
As problem complexity increases the advantage classical computation methods provide plateaus. This limitation primarily stems from the inherent complexity in computationally representing, resolving, and exploring design spaces. This increasing complexity becomes a limitation as we reach the upper end of our manufacturing process limits for classical processors. Despite increasing numbers of transistors the clock speed of classical computers is capped. Further, our ability to store the information returned by our computational tools for further analysis is limited in classical computation. With modern hard disk drives storage capacity in the 10s of TBs we are quickly diverging from what is capable. We are limited by the vastness and complexity of problems – a representation of this problem is shown in the Figure below.
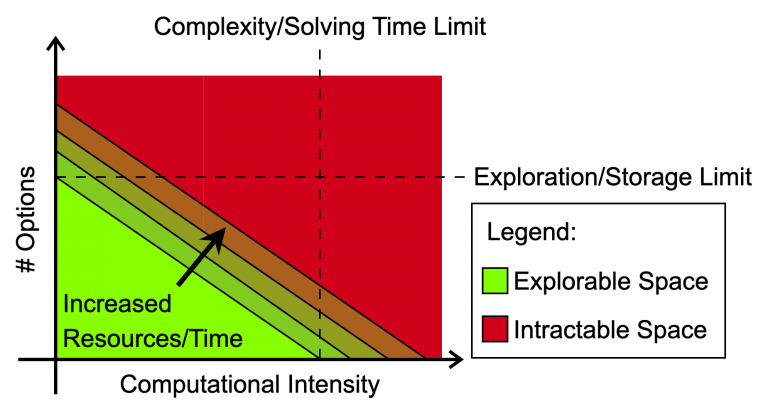
Quantum Computation as the Solution?
These scaling challenges are well known and often encountered in Engineering Design. As a result, research has developed a variety of classical methods to help optimise the exploration of design spaces. Some examples are gradient descent methods, evolutionary algorithms, particle swarm optimisation, and generative approaches. However, these each face their own issues as design spaces become increasingly complex. For example gradient descent struggles with convergence to local optima and traversing discontinuous design spaces.
This begs the question, “Are there a fundamentally different approaches to representing and resolving Engineering Design design spaces such that they can be explored more effectively?”. Quantum Computer Aided Engineering is exploring how Quantum Computing (QC) can provide novel methods of modelling and navigating design spaces. This requires the development reference models for solving Engineering Design problems with quantum algorithms, the design experiments to find promising pairings between problems and algorithms, and a clearer definition the capabilities of today’s devices.
Quantum computers are computers that use quantum phenomena to represent information. The smallest unit of information represented in a quantum computer is a quantum bit – referred to as a qubit. While classical computers process information in binary states (0 or 1), qubits can be in a state of 0, 1, or a superposition of both. This superposition enables quantum computers to perform computations in parallel and explore multiple solutions simultaneously. Taking advantage of superposition, as well as other QC features such as entanglement and tunnelling, has resulted in a number of quantum algorithms for tackling computational problems. However, a gap must be bridged between the available techniques and their implementation. The Figure below compares the operation of two classical and two quantum algorithms, to explain how taking advantage of these phenomena can enable algorithms with a novel operation.
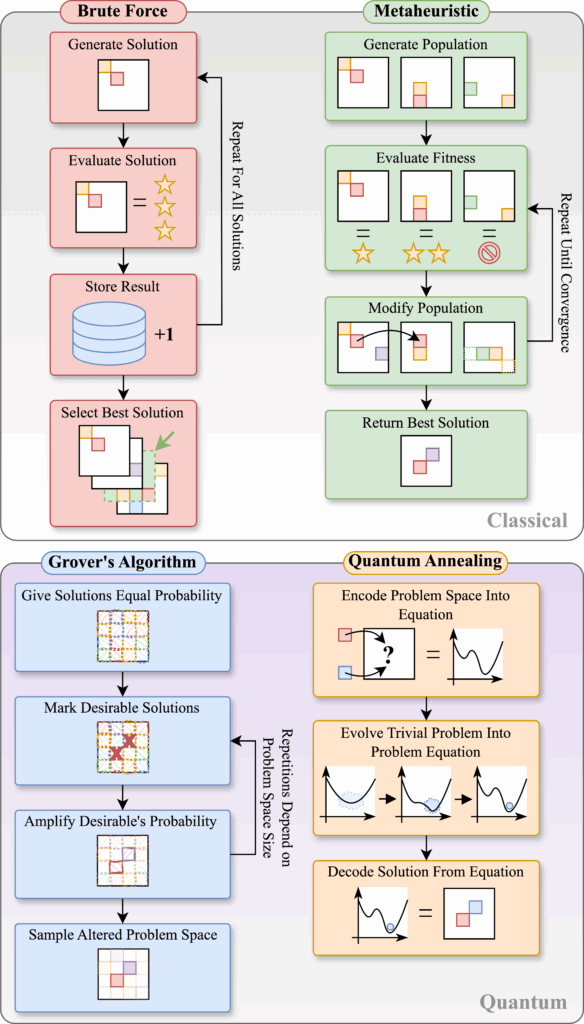
Our Approach (Phase 1)
The first stage of this project (en exploratory study) has now concluded and been published in Design Science under the title “Comparing Gate and Annealing-based Quantum Computing for Configuration-based Design Tasks“. A key feature of the field of QC is that there are many competing hardware options and an overall best approach is yet to emerge. As such, we have been investigating multiple avenues for tackling a classic engineering design problem. A summary of our approach can be seen in the Figure below.
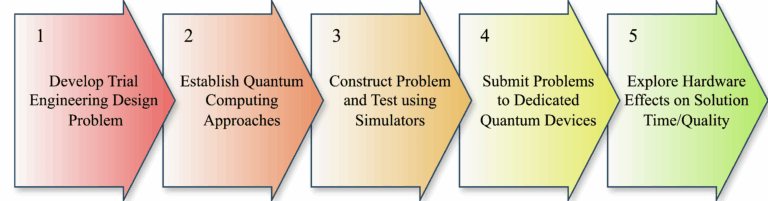
A major challenge in applying QC techniques to engineering design problems is deciding how a solution to the problem should be represented by the qubits used. This problem formulation may change depending on the QC techniques being used to find a solution. Therefore, a key part of our approach was deciding on an appropriate case study problem which would allow comparison between different QC techniques and hardware options.
The problem selected was a form of configuration-design problem. A pictorial representation can be seen below. The problem involves placing two tiles (pink and orange) within the grid. Both tiles must be on the eastern wall of the grid and occupy different spaces. A single objective as included to minimise the horizontal space covered by the tile placements. This problem was chosen as it is an abstraction of many engineering design problems such as factory layout, PCB design, and placement of environmental sensors.
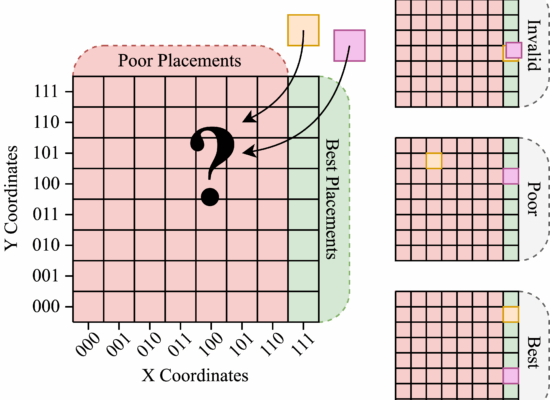
With a case study problem selected, the available QC techniques could be explored and some selected for comparison. For this work, two methods were chosen. These were a gate-based implementation of Grover’s Algorithm using IBM’s quantum devices and Quantum Annealing (QA) implemented using D-wave’s Quantum Processing Unit (QPU).
What is a gate-based implementation of Grover’s Algorithm? Grover’s Algorithm is a quantum algorithm developed for unstructured search through a database. Imagine listing all solutions to a problem (in our case every combination of tile positions). Grover’s Algorithm is able to search this listing and find desirable solutions – ones that meet our constraints. It offers a theoretical quadratic speed up over classical approaches. A gate-based implementation means that Grover’s Algorithm has been implemented using a gate-model quantum computer. These quantum computers can be thought to operate through quantum versions of logic gates. IBM offers cloud access to their gate-model quantum computers through the use of their SDK Qiskit.
How does QA differ from this approach? QA can be thought of as the analogue version of QC and the gate-model as the digital. QA works by formulating your problem in a specific type of equation called a Quadratic Unconstrained Binary Optimisation (QUBO) problem. This QUBO can then be solved via QA using a D-wave QPU and the SDK they provide called Ocean. The key difference between gate-model computation and QA is that QA can only solve combinatorial optimisation problems. However, the hardware supporting QA (D-wave QPUs) is more mature making it a promising avenue for engineering designers despite its limitations.
Our Findings and Next Steps
We compared the two approaches in terms of their time-to-solution, results quality (level of error present in results), and the closeness of the distribution of valid solutions to uniform. We found that only QA produced usable results. We also compared the performance of these approaches to a classical brute force approach. It was found that at increased problem scales QA outperformed this brute force approach in its time-to-solution. As a result of carrying out this exploratory study, we also learned that our method for finding suitable applications for quantum algorithms in engineering design could be improved. Our results made clear the relative infancy of today’s quantum processors. In response to this, we have expanded our research into other quantum algorithms and consulted various experts with the aim of developing a new study. This study will choose a promising near-term quantum algorithm and investigate its performance across a range of problems, flipping the independent variable from algorithms to problem type.
Identifying Suitable Engineering Problems for Quantum Solving: A QAOA Case Study (Phase 2)
We identified the Quantum Approximate Optimisation Algorithm (QAOA) as a suitable case study for our next investigation. This is a variational algorithm, setting it aside from the approaches we have investigated before. Here, variational means that a classical computer is used to enhance a quantum computer by performing a non-trival computation alongside it. This algorithm was selected for its near-term promise and wide applicability in Engineering Design. It is suitable for solving array of optimisation problems similar to quantum annealing. In fact, it requires the same QUBO problem formulation, but it is executed on gate-model hardware.
We chose to formulate several classic NP-hard optimisation problems (Travelling Salesperson, Knapsack, Minimum Vertex Cover, and Maximum Cut) for solving with the QAOA. We then executed the QAOA using an array of ideal and noisy quantum simulators to investigate its performance. We also submitted some jobs to a real quantum computer to enable us to predict solution times for the different problem types. Our aim was to find out “Is there a reliable way to identify what type problem a quantum algorithm is most suitable for?”. We intend to use our result to formulate a robust method for systematically identifying suitable algorithm/problem pairings.
At the time of writing, the experiment has concluded and all results have been collected. A journal paper intended for submission to Transaction on Quantum Engineering is being written.



